Introducción
La cinemática estudia el movimiento de los cuerpos haciendo abstracción de las causas que lo producen. Dicho de otra manera, se ocupa de describir las trayectorias.
El movimiento más sencillo de estudiar es el de una partícula, que es un objeto de cuyo tamaño y estructura se prescinde ya sea porque realmente es muy pequeño o porque a la escala del problema planteado puede considerarse como tal: por ejemplo, la Tierra sería una partícula en los problemas referentes al movimiento planetario.
La posición de la partícula se especifica asimilándola a un punto del espacio (por eso se dice que es un punto material) y dando su vector de posición r o lo que es lo mismo, sus tres coordenadas x , y , z.
Al transcurrir el tiempo la partícula va ocupando distintas posiciones, el conjunto de las cuales constituye la trayectoria del movimiento, que será cierta curva del espacio r(t) = x(t)i + y(t)j + z(t)k. Si el movimiento está limitado a un plano serán suficientes dos de estas funciones del tiempo para definir la trayectoria. Y cuando ésta es rectilínea, basta una sola, x(t) por ejemplo, si los ejes coordenados se toman en la dirección adecuada.
Una curva cualquiera queda definida al expresar el vector de posición r de sus puntos como función de cierto parámetro. Para cada valor del parámetro se obtiene un punto P de la curva.
En particular, podemos utilizar como parámetro la longitud s del arco comprendido entre un punto fijo Po de la curva y P :
La derivada del vector r es tangente a la curva y vale:
El elemento de arco y su cuerda son infinitésimos equivalentes; es decir su cociente tiende a la unidad:
Así pues, la derivada de r(s) resulta ser igual al vector unitario tangente, T. Derivando por segunda vez:
Como T tiene módulo constante su derivada debe ser perpendicular al propio vector, por lo que dT/ds define la dirección normal a la curva. Si designamos por N al vector unitario:
Para calcular el módulo consideremos dos puntos P y Q de la trayectoria separados por un pequeño arco s. Al desplazarse de un punto al otro, tanto el vector tangente como la dirección normal a la curva giran un mismo ángulo (figura 2).
T = TQ - TP se obtiene trasladando TP al punto Q. Del triángulo resultante se deduce que en el límite, cuando s 0, el ángulo |T|/|T| = |T| ya que el arco se aproxima a la cuerda. Por tanto:
El radio de curvatura queda así definido como la derivada del arco respecto del ángulo, ds/d ; es decir, d = ds/ , que es una ecuación similar a la que define el ángulo subtendido por un arco de circunferencia, = s/r. En resumidas cuentas, cada elemento de la curva se puede considerar como un pequeño arco de circunferencia de radio (s).
Sustituyendo el resultado anterior en la ecuación (5) tenemos:
Como ya se dijo en la introducción, la posición de una partícula respecto de cierto sistema de referencia se especifica mediante el vector r(t), que va del origen de coordenadas O a la posición P de la partícula.
En instantes sucesivos t , t' , t'' , ... el extremo del vector determina las posiciones del punto material P , P' , P'' , ... . Por tanto, r es una función del tiempo; en coordenadas cartesianas:
La trayectoria es la curva indicatriz del vector de posición; y x(t) , y(t) , z(t) son las ecuaciones paramétricas de la curva respecto al tiempo, que proporcionan las coordenadas cartesianas del punto en cada instante.
La velocidad es un concepto que da cuenta del cambio de posición de la partícula. Nos dice si ese cambio tiene lugar con mayor o menor rapidez y también la dirección en que se produce.
Si en un intervalo de tiempo Dt la partícula pasa de P a P', el vector de posición cambiara de r a r + Dr. El desplazamiento Dr representa el cambio de posición, no el espacio recorrido, ya que las trayectorias que llevan de P a P' pueden ser distintas. La velocidad media en el intervalo Dt se define como el desplazamiento por unidad de tiempo:
Consideremos, por ejemplo, Dt dividido en dos subintervalos Dt/2. El desplazamiento Dr será la suma de los desplazamientos respectivos: Dr = Dr' + Dr''. La velocidad media se puede poner:
Es decir, vm es la media de las velocidades en los dos subintervalos. Tomando un intervalo de tiempo cada vez más pequeño llegaremos a definir la velocidad instantánea, correspondiente a un solo punto o instante, ya que entonces P' P:
En coordenadas cartesianas la derivada de r se expresa:
La velocidad instantánea es tangente a la trayectoria en P, ya que la derivada de un vector respecto de su parámetro siempre es tangente a la curva indicatriz. Por tanto podemos escribir v como producto de su módulo por el vector unitario tangente:
Así pues, el módulo de v es la longitud de trayectoria recorrida por unidad de tiempo.
Representa la rapidez de la partícula, mientras que T indica la dirección del movimiento. En cartesianas, v es:
En general, la velocidad será distinta en cada punto de la trayectoria: es una función del tiempo. Por ello se introduce el concepto de aceleración como el cambio de la velocidad por unidad de tiempo.
Si tomamos en consideración un intervalo Dt, la velocidad instantánea se incrementa entre P y P' en Dv ; la aceleración media es:
La dirección de am es la misma que la de Dv . Naturalmente, al tomar intervalos cada vez más pequeños obtendríamos distintas aceleraciones medias. Sin embargo la serie tiende hacia un valor que representa la aceleración de la partícula en el preciso instante en que pasa por P:
Es usual representar el movimiento en una dimensión mediante la gráfica x(t). En ella tenemos información sobre las posiciones que va ocupando la partícula y también sobre su velocidad, ya que la derivada de una función en un punto es la pendiente de su gráfica (es decir, la inclinación de la recta tangente a la curva en dicho punto). En este caso la derivada, dx/dt , es la velocidad.
| Ejemplo 1 : La posición de una partícula en función del tiempo está representada en la gráfica de la figura. A partir de ella calcular la velocidad media en los intervalos (3 , 11) y (3 , 7) así como la velocidad instantánea en el punto t = 3. |
Proyectando sobre el eje Ox leemos en la gráfica el valor de los incrementos Dx correspondientes a los intervalos de tiempo del problema. La velocidad media será vm = Dx/t:
| Para calcular la velocidad instantánea se traza una recta tangente en el punto t = 3 y tomando dos puntos cualesquiera sobre ella se determina su pendiente, tg = Dx/t : |
4. Componentes intrínsecas de la aceleración
Se denominan componentes intrínsecas de la aceleración. Para calcular su valor se parte de la ecuación (12), v = v·T y se deriva como un producto:
Sustituyendo en (19) resulta:
Por tanto las componentes intrínsecas son: aT = dv/dt y aN = v2/ . La aceleración tangencial es una medida del cambio de la rapidez del movimiento, pues sólo depende del módulo de la velocidad. La aceleración normal o centrípeta indica un cambio en la dirección de la partícula, asociado a la curvatura de la trayectoria.
En general, aT y aN serán no nulos. Como casos particulares podemos considerar:
En el primer supuesto, con aN = 0, también podría ser nula la aceleración tangencial, en cuyo caso tendríamos un movimiento rectilíneo y uniforme; o bien puede ser aT 0 y entonces la partícula estaría cambiando de velocidad, pero siempre en línea recta.
En el segundo caso, aT = 0, el módulo de v es constante: la rapidez del movimiento es siempre la misma. Si la trayectoria es sinuosa , y por tanto aN , variará de un punto a otro. Pero si el radio de curvatura es constante, aN = v2/R también lo será y tendremos un movimiento circular uniforme.
Cuando a = cte se suele decir que el movimiento es uniformemente acelerado. Pero esto no implica que aT y aN también sean constantes. Así, en el movimiento parabólico de un proyectil las dos componentes de la aceleración varían, aunque su resultante es constante.
Se entiende por movimiento uniformemente acelerado aquél en que la aceleración es un vector constante, a = dv/dt = cte. Para hallar la velocidad se debe integrar dv = adt :
La constante de integración C queda determinada si se conoce la velocidad en un instante cualquiera, que podemos tomar como origen de tiempos, t = 0.
Sea vo la velocidad en el instante inicial. Sustituyendo t = 0 y v = vo en (22) se ve que la constante de integración es la velocidad inicial, C = vo . Por tanto:
Si la velocidad inicial tiene la misma dirección que a, en un instante cualquiera la velocidad tendrá también esa dirección. Por lo tanto el movimiento será rectilíneo, con aN = 0; sólo cambia el módulo de v. Entonces podemos tomar un eje (por ejemplo el Ox) en la dirección de v y el problema queda reducido a una dimensión, con vox = vo y ax = a :
Cuando vo tiene distinta dirección que a el movimiento se desarrolla en el plano que definen los dos vectores, ya que en cualquier instante v será la suma de los vectores vo y a·t, que están en dicho plano.
Si tomamos los ejes de manera que el plano (vo , a) coincida con el plano xy, la componente z será siempre nula y el problema se reduce a dos dimensiones. Más aún, podemos tomar uno de los ejes, por ejemplo el Oy, en la dirección de la aceleración y entonces ax = az = = 0 ; ay = a. Sólo cambiará la componente y de la velocidad, mientras que en la dirección x el movimiento será uniforme:
Para hallar la posición en función del tiempo integramos dr = vdt :
La constante de integración se determina a partir del valor inicial de la posición. Si en t = 0 , r = ro y v = vo , sustituyendo en (26) resulta C = ro . Es decir:
Si el movimiento es rectilíneo (a y vo colineales) la ecuación vectorial anterior queda reducida a una sola componente:
En el caso general el movimiento tiene lugar en un plano (el xy, por ejemplo, con la aceleración en dirección Oy); entonces ax = 0 y ay = a , resultando:
Despejando t = (vy - voy)/a en la ecuación (25) y sustituyendo en y(t) se puede eliminar el tiempo para obtener vy como función de la posición y :
Y sólo hay que desarrollar el cuadrado y simplificar para llegar fácilmente a:
También se puede eliminar el tiempo entre las dos ecuaciones (29) de la posición, de donde resulta la ecuación y(x) de la trayectoria.
| Ejemplo 2 : Se lanza un proyectil con velocidad inicial vo formando un ángulo a con la horizontal. Suponiendo que la única fuerza es la de la gravedad calcular la trayectoria y el alcance del proyectil. Situando el origen de coordenadas en el punto de lanzamiento, xo = yo = 0. Si se sustituye t = x/vox en y(t) tenemos, para a = - g: |
Se a tenido en cuenta que voy/vox = tga y vox = vocosa . La ecuación es de la forma y = Ax2 + Bx + C ; es decir, se trata de una parábola.
Para calcular el alcance hacemos y = 0 y despejamos x = L. Teniendo en cuenta que 2senacosa = sen2a :
| Para una velocidad de lanzamiento dada el alcance se hace máximo cuando a = 45º y vale Lmax = vo2/g. |
6. Movimiento circular
Se dice que un movimiento es circular cuando su trayectoria es una circunferencia. Por tanto, el radio de curvatura es constante y vale = R.
Tomando un radio cualquiera de la circunferencia como referencia para medir los ángulos (figura 10), se define la velocidad angular w como el ángulo girado por la partícula por unidad de tiempo en un instante dado:
La velocidad angular está relacionada con la lineal, ya que s = Rq y ds = Rdq :
Las unidades de w son s-1. Es habitual representar la velocidad angular por un vector perpendicular al plano de la trayectoria cuyo sentido es el que da la regla del tornillo. Así, v es igual al producto vectorial w x R:
La aceleración angular se define como la derivada de la velocidad, w , con respecto al tiempo:
La dirección del vector es la misma que la de , perpendicular al plano de la trayectoria, pero su sentido puede ser igual u opuesto, según esté aumentando o disminuyendo la velocidad.
Las componentes tangencial y normal de la aceleración son:
La aceleración total a se deduce derivando el producto x R :
El movimiento es circular uniforme si el módulo de v es constante; en este caso la aceleración tangencial, dv/dt , será nula. También es constante la velocidad angular = v/R.
El ángulo descrito en función del tiempo se obtiene integrando d = dt :
La aceleración angular, = d/dt, es cero pero no así la aceleración normal, 2R.
El movimiento circular uniforme es periódico. La partícula tarda en pasar dos veces por el mismo punto un tiempo T, que corresponde a un desplazamiento de 2 radianes:
Un punto material con aceleración angular constante tiene una velocidad que varía linealmente con el tiempo:
Integrando d = dt = (o + t)dt tenemos el desplazamiento angular en función del tiempo:
Estas ecuaciones son similares a las del movimiento uniformemente acelerado pero, si bien la aceleración tangencial aT = R es constante, la componente normal aumenta con el tiempo:
7. Movimiento armónico simple
La cantidad t + o se denomina fase del movimiento y su valor en el instante t = 0 es la fase inicial, o . A y son constantes.
Este movimiento (M.A.S.) puede generarse a partir de un movimiento circular uniforme de radio R = A proyectando la posición de la partícula sobre un diámetro de la trayectoria.
Como sen = cos( - /2), la ecuación anterior también se puede escribir:
El ángulo es o - /2. Al desplazamiento x se le suele denominar elongación y a la separación máxima, xmax = A , amplitud de la oscilación.
Al estar definido por la función seno o coseno el M.A.S. es periódico. El periodo T es el tiempo que tarda la partícula en volver a pasar por una posición cualquiera y con la misma velocidad; o sea, x(t) = x(t + T) y v(t) = = v(t + T). Para que la función seno vuelva a repetir sus valores la fase debe incrementarse en 2 radianes, por lo cual:
El número de oscilaciones realizadas en la unidad de tiempo es la frecuencia del movimiento armónico simple, cuya unidad es el hercio:
La magnitud se llama frecuencia angular o pulsación. Sus unidades son radianes por segundo, como la velocidad angular.
La velocidad del punto material se obtiene derivando la función de posición:
La aceleración es la derivada de la velocidad respecto del tiempo:
Es decir, la aceleración es proporcional y opuesta a la elongación (figura 13).





















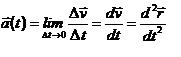













































No hay comentarios:
Publicar un comentario